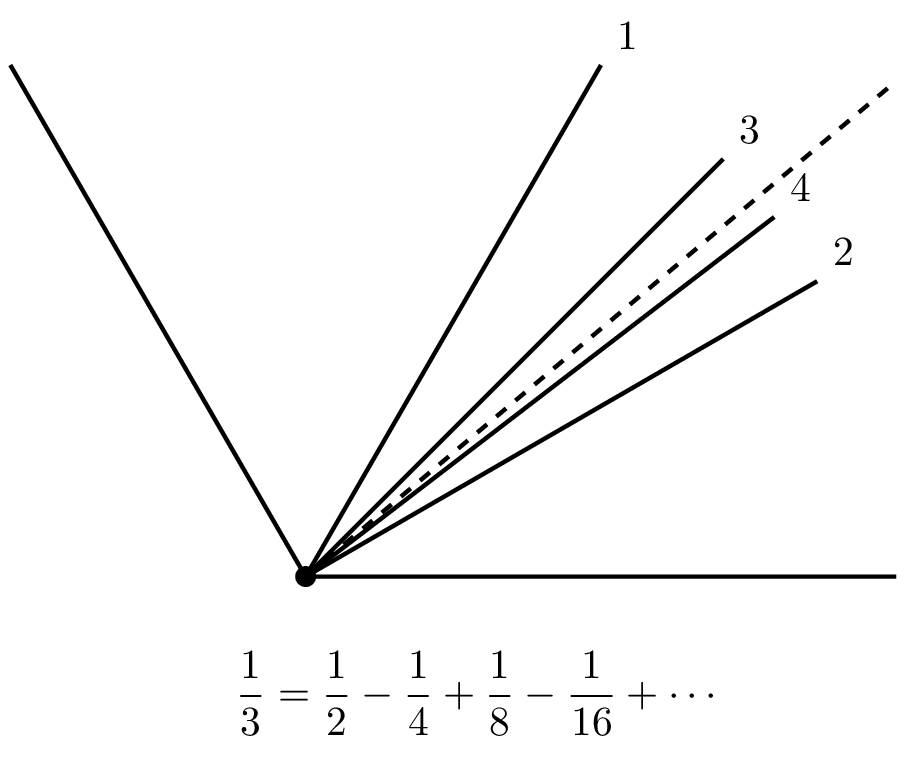
Trisection of an Angle in an Infinite Number of Steps
|
\documentclass[tikz, border=2pt]{standalone}
|
|
\usetikzlibrary{calc}
|
|
\usetikzlibrary{math}
|
|
%\usetikzlibrary{arrows.meta}
|
|
\begin{document}
|
|
\begin{tikzpicture}[line width=1pt]
|
|
\tikzmath{
|
|
\A = 120;
|
|
\l = 5;
|
|
}
|
|
\coordinate (O) at (0, 0);
|
|
\filldraw (O) circle [radius=2pt];
|
|
\foreach \a in {0, \A}
|
|
\draw (O) -- (\a:\l);
|
|
\foreach \a/\i in {0.5*\A/1, 0.25*\A/2, 0.375*\A/3, 0.3125*\A/4}{
|
|
\draw (O) -- (\a:\l) node[above right] {\i};
|
|
}
|
|
\draw[dashed] (O) -- ++(1/3*\A:1.3*\l);
|
|
\node[below=5mm, align=center] () at ($(O)+(0.3*\l, 0)$) {
|
|
$\displaystyle\frac{1}{3}=\frac{1}{2}-\frac{1}{4}+\frac{1}{8}-\frac{1}{16}+\cdots$
|
|
}
|
|
\end{tikzpicture}
|
|
|
|
\end{document}
|


评论
Comments powered by Disqus